- Recognition process presented in
[19]
- The image normalization in [19] was done using this geometry
(the image is from our database)
- Feature Extraction in [19]
- Proposed Classification Process
- The number-plate is detected first. Then the surrounding rectangle is cut from the
image
- Car geometry is measured in the space of number-plate
- ROC curve for evaluated descriptors in [14], here for an rotated image
- Feature representation used for learning
- obtained orientation is modulo
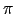 to obtain the same results for (a) and
(b)
to obtain the same results for (a) and
(b)
- Features Extraction
- Possible distinction between random texture and circle-like shapes
- Overlapping Tiles
- These two distributions are very close to each other, but their Euclidean distance is quite large.
- Here is depicted how mass units are transformed from distribution
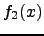 to
to 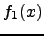 .
.
- Transportation Problem relation to EMD. The solid line shows the minimum work-flow of 2 mass units
- Classification using k-NN,
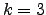 . The test sample T is being classified as
. The test sample T is being classified as 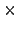 , because in the hypercycle surrounding T are 2 elements from
, because in the hypercycle surrounding T are 2 elements from 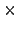 and only one from
and only one from 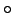 .
.
- Projection from 2D to 1D -- we should be able to find some threshold for classification
- Projection from 2D to 1D -- not a very good projection for classification purposes
- The best is to separate the classes -- projected distances of
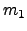 and
and 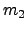 should be maximized and projected scatters
should be maximized and projected scatters 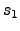 and
and 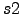 should be minimized.
should be minimized.
- The LDA transformation is trying to maximize
 in the space
in the space 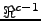
- Sample car images in our database
- Sample truck images in our database
- Optimal Number of Bins
- SIFT Topology and how this influences the classification rate
- SIFT Type and how this influences the classification rate
- EMD vs. Euclidean Distance Function
- The best k for k-NN algorithm
- The explanation to figure 4.7 on page
![[*]](/usr/share/latex2html/icons/crossref.png)
- We can see that SIFT with topology 15x9x25 performed best
- Rotation and stability: (a) sample rotated
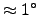 to the left, number of bins equals to 9, (b) sample rotated
to the left, number of bins equals to 9, (b) sample rotated
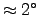 to the right, number of bins equals to 9, (c) sample rotated
to the right, number of bins equals to 9, (c) sample rotated
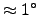 to the left, number of bins equals to 10, (d) sample rotated
to the left, number of bins equals to 10, (d) sample rotated
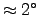 to the right, number of bins equals to 10
to the right, number of bins equals to 10
- SIFTs with higher number of tiles have better classification power but
from certain point the classification rate stagnates
- Here we can see that overlapping SIFTs performed better except
the simplest case
- We can see that EMD and Euclidean distance measures performed almost the
same
- The influence of k on classification rate
- The FLD transformation performed on features extracted from car images
- The FLD transformation performed on features extracted from car
images
- The optimal feature space dimension selection for car images
- The optimal feature space dimension selection for car images
- The training set was reduced to 80% and 60% of its original
size.
- k-NN classifier sensitivity to image blur (truck images)
- SIFT is almost invariant to blur (a) original image, (b) Gaussian with 6x6
region size applied on image
- Images after noise addition. (a)
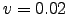 , (b)
, (b) 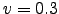
- k-NN classifier sensitivity to image added noise
- In this picture we can see that SIFT discrimination power decreases with
increasing amount of noise. For
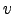 =0.3 the distribution is almost random (d); (a) original
image, (b) added noise,
=0.3 the distribution is almost random (d); (a) original
image, (b) added noise, 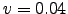 , (c) added noise,
, (c) added noise, 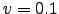 , (d) added noise,
, (d) added noise, 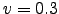
- The training set was reduced to 80% and 60% from its original
size.
- k-NN classifier sensitivity to image blur
- k-NN classifier sensitivity to image added noise
- The Archiecture Overview
- Program Flow
- Feature Extraction Module
- Error Module
- Classification module
Kocurek
2007-12-17