FLD - Fisher Linear Discriminant

Let us assume we have sets $D_i$, these represent $c$ classes, each containing $n_i$ elements ($\vert D_i\vert=n_i$). We are trying to reduce the dimensionality of input data vectors $\mathbf{x} \in D_i$ is $d, d=dim(x)$ to dimensionality $c-1$, where we believe the classification will be more straightforward, maybe possible using linear classifier. We want to do the following transformation:

$$T:\Re^{d} \rightarrow \Re^{c-1}$$ (3.4)

Fisher's Linear Discriminant is trying to maximize the ratio of scatter between classes to the scatter within classes.

Two Classes Classification

First let us illustrate this problem in two classes problem. We can see on figure 3.14 on page that the projection on vector $w_1$ gives us a chance to find some threshold suitable for distinguishing whether a potential test sample belongs to class $D_1$ or $D_2$. This could be possible because the projection of $D_1$ and $D_2$ on $w_1$ results in two separate sets. While on figure 3.15 on page this is not possible because the projected class points from $D_1$ overlap with projected class points from $D_2$. We can see that some projections on vector 1D space are better here and some are worth.

Figure 3.14: Projection from 2D to 1D -- we should be able to find some threshold for classification

Figure 3.15: Projection from 2D to 1D -- not a very good projection for classification purposes

Now take a look at this in more detail. Assume we are trying to project sample $\mathbf{x}$, to scalar value $y$ which corresponds to the metrics of vector $\mathbf{w}$, we are projecting on. This is done by using the following scalar product:

$$y=\mathbf{w}^T \mathbf{x}$$ (3.5)

It is straightforward that if $\mathbf{m_{D_1}}$ is the mean vector for class $D_1$, then its projection on vector $\mathbf{w}$ is:

$$\tilde{m}_{D_1}=\mathbf{w}^T \mathbf{m_{D_1}}$$

The same rule is valid for the scatter. if $\mathbf{s_{D_1}}$ is the scatter matrix for class $D_1$, then $\tilde{s}_{D_1}$ is scatter projected on $\mathbf{w}$:

$$\tilde{s}_{D_1}=\mathbf{w}^T \mathbf{s_{D_1}}$$

What we want to do is:

• maximize the distance of means in the projected space
• minimize all of the scatters in the projected space

We can see figure 3.16 on page that $\mathbf{w_1}$ does this for us:

Figure 3.16: The best is to separate the classes -- projected distances of $m_1$ and $m_2$ should be maximized and projected scatters $s_1$ and $s2$ should be minimized.

We can define the criterion for vector $\mathbf{w}$:

$$J(\mathbf{w})={ \vert\tilde{m}_{D_1} - \tilde{m}_{D_2}\vert^2 \over \tilde{s}^2_{D_1} + \tilde{s}^2_{D_2} }$$ (3.6)

We want such a $\mathbf{w}$ to maximize the function $J(\mathbf{w})$.

Now we can define scatter matrices. First define scatter within classes matrix:

$$\mathbf{S_W}=\sum{S_{D_i}}$$ (3.7)

where $\mathbf{S_{D_i}}$ is defined as:

$$\mathbf{S_{D_i}}=\sum_{\mathbf{x} \in D_i}{ (\mathbf{x} - \mathbf{m_{D_i}})(\mathbf{x} - \mathbf{m_{D_i}})^T }$$

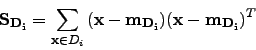
We can easily see that:

$$\tilde{s}^2_{D_i}=\mathbf{w}^T\mathbf{S_{D_i}}\mathbf{w}$$

We define scatter within classes as the sum of all class scatters. We are trying to find a projection where these scatters are as small as possible (see figure 3.16 on page ). This is done by $\mathbf{w}^T\mathbf{S_W}\mathbf{w}$.

We define scatter between classes for two classes (we will change its definition later in Multiple Classes Classification as:

$$\mathbf{S_B}=(\mathbf{m_{D_1}} - \mathbf{m_{D_2}})(\mathbf{m_{D_1}} - \mathbf{m_{D_2}})^T$$

This defines the distance between means of class $D_1$ and class $D_2$. We are trying to find a projection where this is as distant as possible (see figure 3.16 on page ). This is done by $\mathbf{w}^T\mathbf{S_B}\mathbf{w}$.

The maximization of mean distances and minimization of class scatters is done by maximizing $J(\mathbf{w})$ which we can now rewrite as:

$$J(\mathbf{w}) = { \mathbf{w}^T\mathbf{S_B}\mathbf{w}\over \mathbf{w}^T\mathbf{S_W}\mathbf{w}}$$ (3.8)

In fact equations (3.8) and (3.6) are the same.

Multiple Classes Classification

As stated in (3.4) FLD does the dimensionality reduction for us. In multiple classes classification we want to project to space $\Re ^{c-1}$, where $c$ is the number of classes we have: $D_1, D_2, \dots, D_c$.

We will leave the definition of $S_W$ unchanged but we have to change the definition of $S_B$. We will define total mean as:

$$\mathbf{m} = {1 \over N} \sum_{i=1}^c{n_i\mathbf{m_{D_i}}}$$ (3.9)

which is in fact center of gravity of all class means $\mathbf{m_{D_i}}$ and if the mean is computed using the proper statistic^3.1 $\mathbf{m}$ is the center of gravity of all $\mathbf{x} \in {D_1, D_2, \dots, D_c}$

Then we can define scatter between classes as:

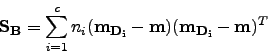$$\mathbf{S_B}=\sum_{i=1}^c{ n_i(\mathbf{m_{D_i}} - \mathbf{m})(\mathbf{m_{D_i}} - \mathbf{m})^T}$$ (3.10)

Now what we are going to do is:

$$\mathbf{y} = \mathbf{W^Tx}$$ (3.11)

where $\mathbf{y}$ is a projection of $\mathbf{x}$ in $\Re ^{c-1}$ space, $dim(\mathbf{y})=c-1$ and $\mathbf{W}$ is matrix of $(c-1)$ x $d$.

We are trying to maximize $J(\mathbf{W})$ defined very similarly to (3.8):

$$J(\mathbf{w}) = { \mathbf{W}^T\mathbf{S_B}\mathbf{W}\over \mathbf{W}^T\mathbf{S_W}\mathbf{W}}$$ (3.12)

As we can see on figure 3.17 on page LDA transformation is trying to spread classes across $\Re ^{c-1}$.

Figure 3.17: The LDA transformation is trying to maximize $d_1^2+ \dots +d_c^2$ in the space $\Re ^{c-1}$

Solving Fisher's Discriminator

We can mark $\mathbf{w_i}$ as columns of $\mathbf{W}$ in (3.12). Then we need to solve the generalized eigenvalue problem:

$$(\mathbf{S_B}- \lambda\mathbf{S_W})\mathbf{w_i} = 0$$ (3.13)

The is the same as:

$$(\mathbf{S^{-1}_W}\mathbf{S_B}- \lambda\mathbf{E})\mathbf{w_i} = 0$$ (3.14)

We can use this by Singular Value Decomposition which is implemented in many mathematical programs and libraries.

Once we have the projection matrix $\mathbf{W}$ we can do the classification in space of dimension $\le c-1$ by projecting test sample to this space and finding the maximum for $p(x\vert D_i)P(D_i)$. Another approach can be using Nearest Neighbor in this reduced space.

Implementation

We can use svd(inv(Sw)*Sb) function implemented in Matlab or PDL::MatrixOps or ccmath. When using Matlab we can also use eig(Sw,Sb) function which can solve the generalized eigenvalue problem.

Possible Issues

The main issue here is that $\mathbf{S^{-1}_W}$ can be singular when we have a high-dimensional data (which is usually true for images) and not enough train data supplied. E.g. in our case we have 32 SIFT tiles each has 9 bins which is in result a vector of dimension 288. Thus $\mathbf{S_W}$ and $\mathbf{S_B}$ are matrices $288$x$288$. In an ideal case we would need $288^2$ of train pictures[6] to not have $\mathbf{S^{-1}_W}$ degenerated.

The possible solution is to use Principal Component Analysis(PCA) first[5,6,7], but the problem is that vectors containing a very important information could be part of PCA null space^3.2[5,6].