Earth Mover's Distance -- EMD

The Earth Mover's Distance(EMD) was introduced in [8]. The problem of Euclidean distance is that when we have features such as SIFT, then the two direction distributions are almost the same or at least very similar to each other (see figure 3.10 on page ).

Figure 3.10: These two distributions are very close to each other, but their Euclidean distance is quite large.

The Earth Mover's Distance is the minimum amount of work needed to transform one distribution to another one. We assume that both distributions have the same mass, in our case:

$$\int_{-\infty}^{+\infty}{f(x)dx} = 1$$

Figure 3.11: Here is depicted how mass units are transformed from distribution $f_2(x)$ to $f_1(x)$ .

In the case on figure 3.10 on page the Euclidean distance would be $2^2+0+0+0+0+2^2 = 4$, the EMD is only 2 (see figure 3.11 on page ).

Figure 3.12: Transportation Problem relation to EMD. The solid line shows the minimum work-flow of 2 mass units

What we need to solve is Transportation Problem. We have a bipartite graph (figure 3.12 on page ), one side of nodes represents consumers ($C$), the second one producers ($P$). We want to find such a flow $f_{ij}$ which minimizes the overall cost $c_{ij}$ between transporting mass from producers to consumers:

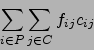$$\sum_{i \in P}\sum_{j \in C}{f_{ij}c_{ij}}$$ (3.2)

In our case $c_{ij}$ is defined as:

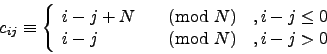$$c_{ij} \equiv \left \{ \begin{array}{lll} i-j+N & \pmod N &, i-j \leq 0 \\ i-j & \pmod N &, i-j>0 \\ \end{array}\right.$$ (3.3)

which reflects that the very left and the very right bins are neighbors.